Combien de poissons faut-il pour former un banc ?
Cette question insolite intriguait des chercheurs britanniques et allemands, au point d'en faire l'objet d'une étude scientifique. Cette dernière montre que même avec un petit nombre d'individus, un groupe de poissons peut présenter des similitudes avec d'autres dix fois plus grands.
Il est fréquent de voir les poissons se déplacer en banc, ces groupes constitués d’un nombre potentiellement élevé d’individu. Dans une étude publiée dans la revue Nature Communications le 22 mars 2024, des chercheurs de l’université de Bristol (Royaume-Uni) et de l’université de Düsseldorf (Allemagne) se sont posé la question insolite suivante : combien faut-il de poissons pour constituer un banc ?
Les mouvements des poissons captés par des caméras
Pour étudier la question, les chercheurs ont placé des groupes de 2 à 50 poissons zèbres (Danio rerio), poissons fortement étudiés du fait de leur praticité d’utilisation en laboratoire, dans un aquarium de l’université de Bristol.
Les mouvements des poissons ont été capturés à l’aide de plusieurs caméras synchronisées. Cet assemblage de caméras permet de reconstruire la trajectoire de chaque poisson en trois dimensions.
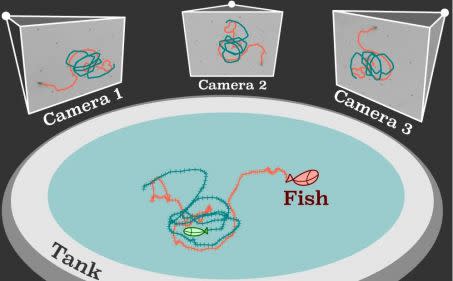
Schéma de l'expérience faite à Bristol. Crédits : A. Zampetaki, Y. Yang, H. Löwen et C. Patrick Royall dans Nature Communications
Avec ces trajectoires, les chercheurs ont pu étudier les changements de comportement dans le déplacement des poissons en fonction du nombre d’individus qui constituaient le groupe.
Lire aussiIntelligence collective : ces champions de la synchronisation
Des méthodes de physique statistique
Pour caractériser les comportements des poissons, les chercheurs ont utilisé des outils de mécanique statistique et de physique de la matière active, domaine étudiant des ensembles de composants en interaction.
Ils ont ainsi étudié les corrélations spatiales à deux corps, c’est-à-dire la probabilité qu’un poisson se trouve à une position donnée par rapport à un autre poisson. Ils ont également regardé les corrélations à trois corps, la probabilité de positionnement d’un troisième poisson relativement à deux poissons déjà placés.
Ils ont également mesuré deux paramètres caractérisant l’état du système de poissons. Ces deux paramètres quantifient respectivement l’alignement des poissons (Op) e[...]
Lire la suite sur sciencesetavenir.fr

 Yahoo Actualités
Yahoo Actualités 